
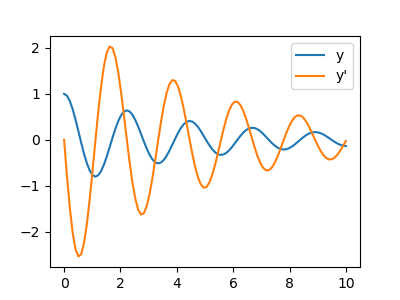
I now solve $\frac$ is of course, again, singular. So I thought of finding another point to start integrating from which should be on the same trajectory as in the original case above. How can I ensure that the numerical solution is monotonically increasing? import numpy as npĪs Geoff Oxberry mentions in his answer the RHS of the ODE is infinite at the initial condition. However on closer inspection we see that it is not: I’ve used it more, and I find it easier to work with whenever there’s an actual dataset that I’m shifting around, not just pure numeric values.The solution to the ode below looks like it is monotonically increasing: I know all the cool kids on the Python block are using matplotlib. So when actually solving these analytically, you don’t think about it much more once you know whether the c.e. If you go look up second-order homogeneous linear ODE with constant coefficients you will find that for characteristic equations where both roots are complex, that is the general form of your solution. This equation might look duanting, but it is literally just straight-from-a-textbook material on these things. I’m looking forward to pushing Python’s numeric/mathematical capabilities further in the future. SciPy has more advanced numeric solvers available, including the more generic for dealing with more complicated equations.īut overall, considering I had never used Python to solve this sort of thing before, I’m pretty impressed by how easy it was to work through this solution.
#Scipy odeint how to#
We could have done this for an equation even if we don’t remember how to solve it ourselves, as long as we’re able to reduce it to a first-order ODE system like here. I’ll add that the Python solution here is not just a mere plot of the analytic method. > approx plot(y ~ t, data=approx, type= 'l') We can pretty much just ignore the \(t\) argument and write To do this we need to write a function that takes a matrix \(Y\) and a time \(t\) and returns a new matrix with the values of \(x_1', x_2'\) for that time.
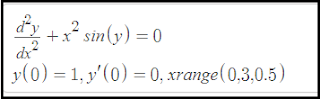
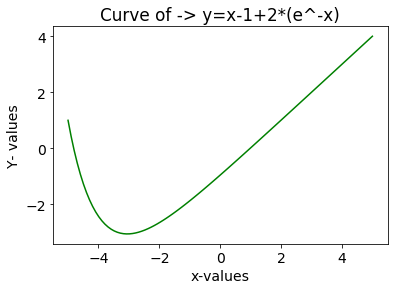
So our characteristic equation here is \ and its roots \(r_ \] which we can pretty much just plug into directly. Regardless, I’ll go over the exact analytical answer, since it’s pretty easy to find in this case.Īn equation of the form \ where \(\alpha\), \(\beta\), \(\gamma\) are some constants, has a characteristic equation \ Once we have this characteristic equation we can avoid actually doing any calculus and just solving that quadratic. If you’ve taken a class on ordinary differential equations, then you should recognize this as a second-order linear homogeneous ODE with constant coefficients. Depending on what we’re trying to do with the answer, the numeric solution might be all that we need. Our analytic solution will let us write an equation for \(y\) that’s solvable for any time \(t\), but the numeric solution in Python will just give us answers in some range that we actually calculate. Generally speaking, this is only one small part of a real-life circuit problem: you know that when you flip some switch, the circuit can be simplified to the above equation and that lets you solve it for some range \(t_1 < t < t_2\), where \(t_1\) and \(t_2\) are the time boundaries where you didn’t have the switch thrown. In real life, this sort of problem often comes up when you’re dealing with a circuit containing a capacitor that discharges through an inductor over time, and you want to analyze the voltage or current going through any given part of the circuit while this happens. Can we write an equation for \(y\), or at least get some answers about its behavior? I gave it a shot for one of the simpler equations, and here are my results (with analytic solution included for comparison). I was going through my ODE notes the other day and wondered if I could solve any of them with Python.


 0 kommentar(er)
0 kommentar(er)
